Theory:
FFT is a most efficient algorithm used in speech processing, frequency estimation and communication. FFT utilizes full advantage of two symmetry properties in order to provide efficient algorithm for DFT. while considering a divide and conquer approach, a computationally efficient algorithm can be developed. This methods depends on the decomposition of an N-point DFT into successively smaller size then DFTs. While in the N-point sequence, the term N can be expressed as N = r1r2r3, …, rm, then N = r m, can be decimated into r-point sequences For each r point sequence, r-point DFT are often computed. Hence the DFT is of size r. if the number r is called the radix of the FFT algorithm while the number m indicates the number of stages in computation. If the value of r = 2, it is called radix-2 FFT.
Steps involved in finding the FFT of the given sequence:
- Let’s consider an input sequence as x[n].
- Let’s find the length for the input sequence using length command.
- In order to find FFT and IFFT by using the matlab commands fft and ifft.
- Let’s plot the magnitude and phase response for the given sequence.
- And finally display the results.
Program:
clc;
clear all;
close all;
x=input(‘Enter the sequence : ‘)
N=length(x)
xK=fft(x,N)
xn=ifft(xK)
n=0:N-1;
subplot (2,2,1);
stem(n,x);
xlabel(‘n—->’);
ylabel(‘amplitude’);
title(‘input sequence’);
subplot (2,2,2);
stem(n,abs(xK));
xlabel(‘n—->’);
ylabel(‘magnitude’);
title(‘magnitude response’);
subplot (2,2,3);
stem(n,angle(xK));
xlabel(‘n—->’);
ylabel(‘phase’);
title(‘Phase response’);
subplot (2,2,4);
stem(n,xn);
xlabel(‘n—->’);
ylabel(‘amplitude’);
title(‘IFFT’);
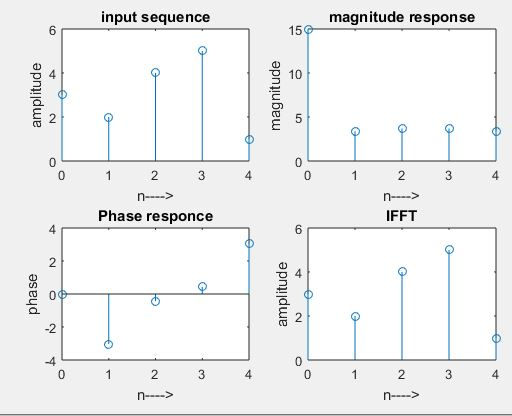
Output:
Enter the sequence: [3 2 4 5 1]
x = 3 2 4 5 1
N =5
xK =15.0000 + 0.0000i -3.3541 – 0.3633i 3.3541 – 1.5388i 3.3541 + 1.5388i -3.3541 + 0.3633i
xn =3.0000 2.0000 4.0000 5.0000 1.0000