Cell traffic load is typically characterised has the two important distributed parameters.
- Average number of mobile stations requesting the service (average call arrival rate (λ).
- Average length of time the mobile stations requiring the service (average holding time T).
The offered traffic load is defined as
a= λT.
For example, in a cell with 100ms, on average, if 30 requests are generated during an hour with an average holding time of T=360 seconds then the average call arrival rate is.
λ =
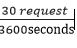
A servicing channel that is kept busy in an hour is quantitatively defined as one ERLANG.
Here the traffic load offered for the example by ERLANG is
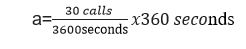
= 3 Erlang.
The average arrival rate is λ and the average departure rate is µ. Therefore all the channels are busy, for this arriving call is turned away. An M/M/S/S queuing model of the system can be analyzed. Since M/M/S/S is a special case of M/M/S/∞, steady-state probabilities p(i) for these systems have the same form as those for states i=0…S in the M/M/S/∞ model. Therefore, S is defined as the channels in a cell. Thus we have
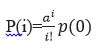
Where a= λ/µ is the offered load and
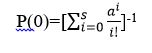
Therefore the arriving call probability p(s) blocked is equal to the probability of all the channels are busy, which is
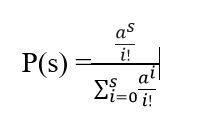
The above equation is called the Erlang B formula and is denoted by B(s, a). B(s, a). Therefore it also called blocking probability of rejection, or probability of loss.
From the old example, if S is given as 2 with a=3, the blocking probability is
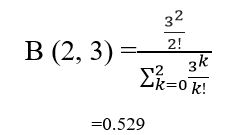
Therefore, a fraction of 0.529 calls is blocked, and that we got to reinitiate the decision. Thus the entire number of blocked calls is about 30*0.529=15.87. The efficiency of the system is often given by.

